写在前面：这是一个很有意义的一节课，在哈佛大学的CS50X计算机入门课后，这是对二进制数值系统更加深入的一门课。

大量计算机的安全漏洞都是由于计算机算术运算的微妙细节引发的，也有是对于数值范围的不了解和不负责引发的。
波音 787 的电力控制系统在 248 天电力不中断的状况下会自动关机，这是由于其使用了32位整形Integer，248天的来源是因为一个int的最大值是2147483647，2147283647 / (60 60 24) = 248.55天，这就是bug的来源（一个不小心，bug又多一个。当然，知道怎么避免bug，随手写点小bug也就很顺理成章了，详情请见防御性编程）

信息存储

字数据大小

为什么现在大部分系统的一个字节是8个比特？你是不是觉得这是理所当然的？【伯克利CS61C】计算机架构的伟大思想 (RISC-V基金会主席Krste亲自授课)
这门课上就有人问了这个问题（CS61ABC系列也是UCB的神课，有空可以去看看），教授指出：最终决定一个字节大小是8个比特的，是1964年出现的大名鼎鼎的 IBM System/360，当时IBM为System/360设计了一套8位EBCDIC编码，涵盖了数字、大小写字母和大部分常用符号，同时又兼容广泛用于打孔卡的6位BCDIC编码，System/360很成功，也奠定了字符存储单位采用8位长度的基础，这就是1字节=8位的由来。
在近年来随着计算机的发展，很多程序都在进行32位到64位的迁移（当然在古老的单片机上可能还有16位的存在）在不同系统下的变量定义可能导致数据溢出的问题。可以根据下表知道，相同类型在不同的程序位数里其内存大小是不一样的（因此学校里C语言考试闲着没事就问你内存大小并且不指定程序位数是没有任何实际意义的）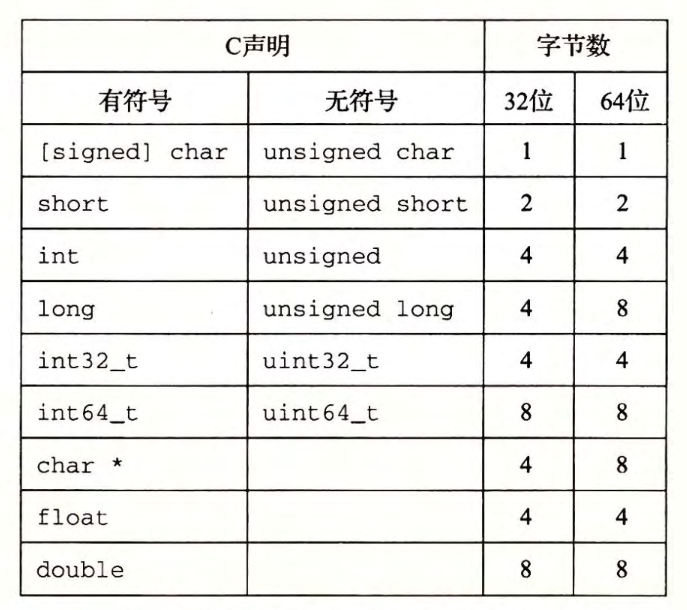
image.png
使用确定大小的整数类型是程序员准确控制数据表示的最佳途径，不同类型会产出各种奇怪的bug，比如：许多程序员假设一个声明为int类型的程序对象能被用来存储一个指针。这在大多数32位的机器上能正常工作，但是在一台64位的机器上却会导致问题。

字节顺序

在逆向中会接触许多汇编，字节顺序会变得很重要，除非遇上二进制回文数，不然你也不想大端序和小端序搞错了导致数字翻译错误对吧。
在学校的C语言教材中，大端序和小端序的引入是在 union中引入的，是因为union允许以一种数据类型引用一个对象，而这种数据类型与创建这个对象时定义的数据类型不同，这在系统级的编程中是必要的，但是平时就算了，容易写BUG。那么怎么用union呢，可以在下面的例子中提供一定参考。

简单例子
1
2
3
4
typedef union{
	char data;
	short int color_tab;
}color_tab;

由于是8bit的图片，这个图片的head将是一个16bit的索引，也就是调色板（具体这些定义可以自行查找rgb以及bmp的资料），它将和具体的索引值一起存在union中。
节省系统内存空间和转换的代码量

检测系统端序
1
2
3
4
5
6
7
8
int is_little_endian(void){
	union w{
		int a;
		char b;
	}c;
	c.a = 1;
	return (c.b == 1); // 小端返回TRUE,大端返回FALSE
}
链表

在写代码之前，我们先回顾一下 union的定义：

  1. 联合定义的最大空间是它的成员最大的那个变量定义。
  2. 将保证对最小成员的类型进行强制的对齐。
    1
    2
    3
    4
    5
    6
    7
    8
    struct node{
    	int size;
    	struct node *p_node;
    }
    typedef union{
    	struct node node_t;
    	int align_x;
    }node_u;
    将单链表做了强制的按照int的对齐

利用语言和语句的特性来进行我们代码的优化以及提高系统的鲁棒性。

表示字符串

可以用 ASCII码来表示英文字符。如果解码和编码采用不同编码方法，将导致 “锟斤拷”。做过misc的人应该深有感触。

表示代码

不同的机器类型使用不同的且不兼容的指令和编码方式。即使是完全一样的进程，运行在不同的操作系统上也会有不同的编码规则，因此二进制代码是不兼容的。二进制代码很少能在不同机器和操作系统组合之间移植，具体过程请见编译原理。
点你呢，Linux，不同发行版的二进制都不统一了。
逻辑运算和布尔代数的内容在这里不做任何评价，学习过C语言的应该对这些内容感到相当熟悉，需要注意的是逻辑右移和算术右移的区别，编码别搞错了。

整数运算

整形的结构：原码，补码，反码的规则应该已经考烂了，补码 = 反码 + 1，今天来讲讲其他的。

强制类型转换

强制类型转换只是把当前地址段的相同内容做了不同的译码处理，这就是为啥把一个整形转换成浮点型数字，他的值不是原来的原因，因为他们的编码规则并不相同。

隐式类型转换

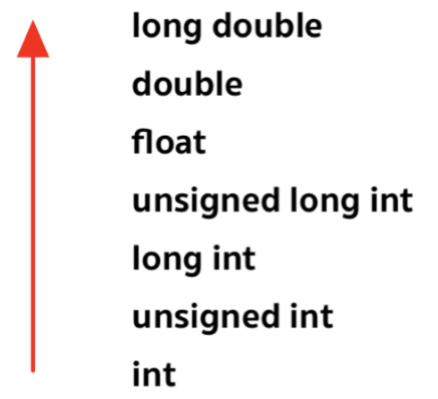
image.png
类型转换的顺序如上。我愿意称其为：BUG的根源。下面用书上练习2.25的代码例子进行更进一步的说明。

1
2
3
unsigned int length;int res = 0;
for(int i = 0 ; i <= length-1; i++)
	res += a[i];

显然，理想中，当length = 0 时，res的值应该是0，但是在这里，length是无符号类型，0-1 = 0xFFFFFFFF，这就发生了错误。
当然很多人会说：我才没有这么傻，这么简单的错误我才不会犯。但是看看下面的代码有没有中招：
1
2
3
char s[10];
for(int i = 0 ; i <= strlen(s)-1 ; i++)
	do something.....

strlen的返回值是无类型的，其函数原型为：unsigned int strlen(const char *str);
你看，这不就中招了，这代码写的和上面的练习并没有什么区别。而且 strlen 也是一个危险函数，他会在检测到\0的时候得到函数的长度，但是可以用其他软件注入一个含有\0的字符串，同时长度很长。可以绕过其安全检查机制，并造成内存溢出。

整形溢出

高德纳在《计算机程序设计的艺术》指出，虽然早在1946年就有人将二分查找的方法公诸于世，但直到1962年才有人写出没有bug的二分查找程序，可见，写一个安全的代码并不容易。如果一提到二分法就毫不犹豫的写下了如下的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int binary_search(int a[], int len, int key){
	int low = 0;
	int high = len - 1;
	while ( low <= high ) {
		int mid = (low + high)/2; // 提示：这里有溢出Bug！
		if (a[mid] == key) {
			return mid;
		}
		if (key < a[mid]) {
			high = mid - 1;
		}
		else{
			low = mid + 1;
		}
	}
	return -1;
}

那么恭喜你，写的还是一个BUG，那么怎么避免呢，其实很简单，把有整形溢出Bug的地方改成没有就可以了。多一步计算，多一份安心。
1
int mid = low + (high - low) / 2;//你看，这就没整形溢出的BUG了

那么怎么检测整形溢出呢，先看看书上代码吧
1
2
3
4
int tadd_ok(int x, int y){
	int sum = x + y;
	return (sum - x == y ) && (sum - y == x)
}

首先，这是一个有问题的代码，因为补码加减应用的是模数运算，模数加法（减法可以转化为加法）形成阿贝尔群(Abelian group) 阿贝尔群满足交换律和结合律 ，这个运算在数学本质上可以看出是不存在问题的。
因此比较直观的方式是：(整形分为正溢出和负溢出)
1
2
3
4
5
6
int tadd_ok(int x, int y) {
	int sum = x + y; 
	int neg_over = x < 0 && y < 0 && sum>= O; 
	int pos_over = x >= 0 && y >= 0 && sum< O;
	return !neg_over && !pos_over;
}

浮点数

浮点数的结构：IEEE SA - IEEE 754-2008官方文档，其设计的还是比较优雅的。
image.png
当然，各家也有自己的浮点数标准：bfloat16 floating-point format - Wikipedia这是谷歌花大力气自己搞的一套标准。
下面还是解释一下IEEE的浮点数标准，以float为例。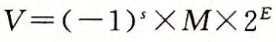
image.png

  • s，符号（sign）：s 决定这数是负数（s = 1)还是正数。数值为0作特殊处理。
  • M，尾数（significand）：M是一个二进制小数，它的范围是[1,2）,或者是[0,1)
  • E，阶码（exponent）：E的作用是对浮点数加权，这个权重是2的E次幕（可能是负数）。
    image.png

    平方根倒数快速算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float Q_rsqrt(float number){
	long i;
	float x2,y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y = number;
	i = * (long * ) & y;
	i = 0x5f3759df - (i >> 1);
	y = * (float *) & i;    
	y = y * (threehalfs - (x * y * y));    //牛顿迭代法
	y = y * (threehalfs - (x * y * y));    
	y = y * (threehalfs - (x * y * y));      
	return number * y;
}

牛顿迭代法

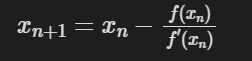
image.png
求根号时，f(x) = x^2， 迭代次数取决于初始值的选择，因此，想要用好牛顿迭代法求开根号，关键在于初始值的选取。

再次理解float

上面那个浮点数表示公式的意义也仅仅是公式，实际上，在执行起来的过程中，我们还有许多实现的细节。
比如阶数exponent，在实际中，他用8位二进制表示[0,255]，然而这不是我们想要的，因为还有可能这个数很小，需要指数是一个负数，所以在实际操作中我们会将其减去127，使其表示范围为[-127,127]
浮点数的第三部分存储的是M，电脑首先存储的是小数点后的位置，在需要的时候把前面的1.加上，1.存储时省略，然后转换成10进制。也就是说，下面这张图代表的数字是1.5。
image.png
使用通用公式表示如下：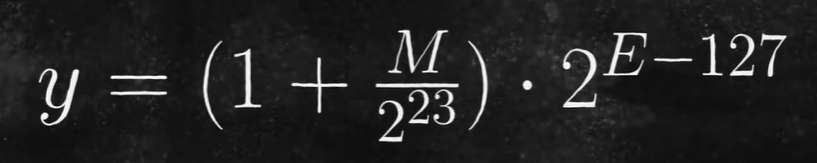
image.png

设计算法

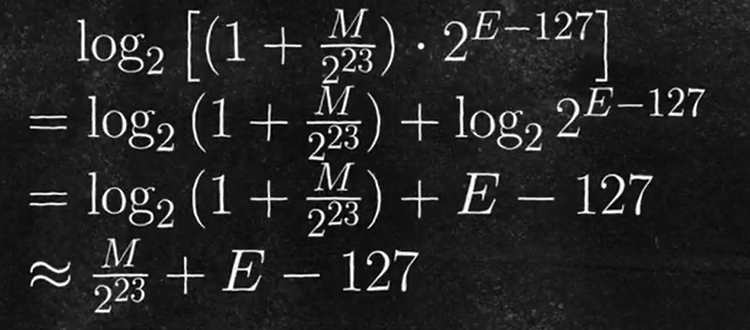
image.png
在这里，我们利用了无穷小量替代的方式，在这里进行了一次替代，但是这个替代是误差过大的，因此不够精确，但是不重要，先看看这个误差大的方法后续是什么步骤。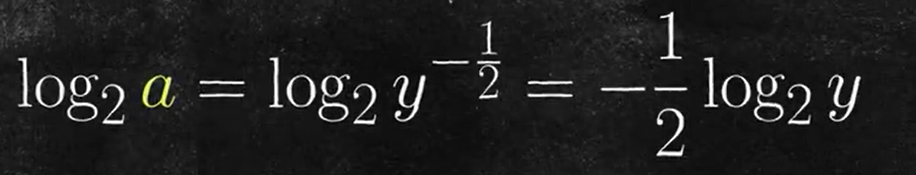
image.png
其中，a是y的平方根倒数，那么把其二进制形式代入，是可以轻易得到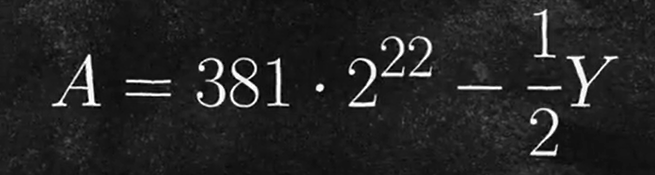
image.png
也就是上面这个代码：i = 0x5f4000000 - (i >> 1);的来源，但是误差过大，因此略微调整后，就是如今的快速迭代算法。

拓展阅读

侧信道攻击

指基于从计算机系统的实现中获得的信息的任何攻击 ，而不是基于算法本身的弱点，比如定时信息，功耗，电磁泄漏甚至声音都可以提供额外的信息来源，被 “黑客” 加以利用，说白了就是以「旁敲侧击」的方式进行攻击。

1
2
3
4
5
6
7
8
9
10
int memcmp(const void *s1, const void *s2, size_t n) {
    if (n != 0) {
        const unsigned char *p1 = s1, *p2 = s2;
        do {
            if (*p1++ != *p2++)
                return ((*--p1) - (*--p2));
        } while (--n != 0);
    }
    return (0);
}

在上述代码中，假如我们有办法精确记录这个函数执行所耗费的时间，那不就可以大概知道在哪个字符出现了不匹配吗？这样的话密码破解的难度将大幅降低。因此涉及密码学和处理敏感信息的程序应该引入常数时间的实现。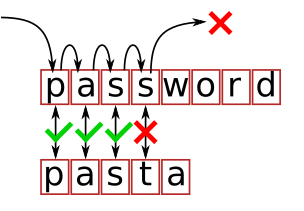
image.png

位运算的奇技淫巧

Bit Twiddling Hacks (stanford.edu)

C语言安全代码规范

华为C语言编程规范 | wiki (gitbooks.io)

有品位的代码

删除一个链表：初学者版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void remove_list_node(List *list, Node *target)
{
    Node *prev = NULL;
    Node *cur = list->head;
    // 遍历链表
    while (cur != target) {
        prev = cur;
        cur = cur->next;
    }
    // 删除节点
    if (!prev)
        list->head = target->next;
    else
        prev->next = target->next;
}

有追求的代码：
1
2
3
4
5
6
7
8
9
10
11
12
// 有品位的版本，消除特例，简单优雅的代码
void remove_list_node(List *list, Node *target)
{
    // The "indirect" pointer points to the *address*
    // of the thing we'll update.
    Node **indirect = &list->head;
    // Walk the list, looking for the thing that 
    // points to the node we want to remove.
    while (*indirect != target)
        indirect = &(*indirect)->next;
    *indirect = target->next;
}